Hlm Missing Data Found at Level 1 Unable to Continue
This page is archived and no longer maintained.
This seminar covers the basics of two-level hierarchical linear models using HLM 6.08. We will use data files from the High School and Beyond Survey. The data files in SPSS format come with HLM software and are located in the subfolder /examples/Chpater2 of the HLM folder.
Outline
- Getting data into the HLM program
- ASCII files
- files from common statistical packages
- The data set
- description of example data set and where to find it
- a brief word about sample size
- Model building
- unconditional means model
- regression with means-as-outcomes
- random-coefficient model
- intercepts and slopes-as-outcomes model
- graphing the results
- Model fit
- model checking based on the residual file
- testing homogeneity of level-1 variances
- multivariate hypothesis tests of fixed effects
- multivariate tests of variance-covariance components specification
- Other issues
- modeling heterogeneity of level-1 variances
- models without a level-1 intercept
- constraints of fixed effects
- testing multi-degree-of-freedom variables
- using probability weights
- multiply imputed data files
Getting data into HLM
Getting data into HLM 6.08 is much easier than it was in earlier versions. Previously, the data for the level 1 variables had to be in one data file, and the variables for level 2 had to be in a different data file. Now, both level 1 and level 2 variables can be in the same data file. It is very easy to bring in SPSS, SAS and Stata (including version 11) data files using the Input File Type pull-down menu.
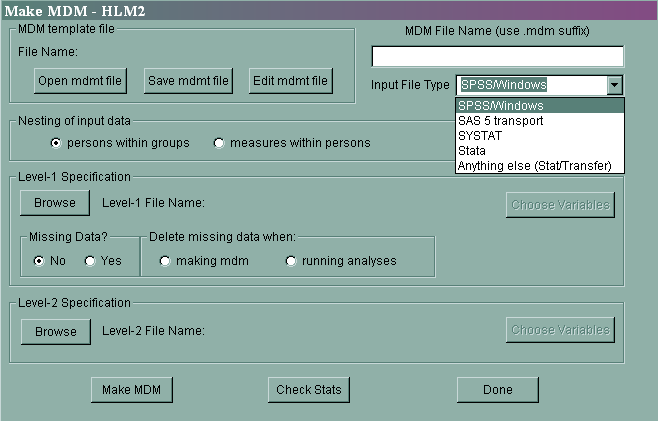
Missing data are often an issue with multilevel data. HLM will allow missing values at level 1, but it will not allow missing values at level 2. If you have missing data at level 2, you will want to remove those cases before you bring your data into HLM. Alternatively, if you have multiply imputed data files, you can use those. A brief example will be shown at the end of the seminar.
The data set
Our data file is a subsample from the 1982 High School and Beyond Survey and is used extensively in Hierarchical Linear Models by Raudenbush and Bryk. The data file, called hsb, consists of 7185 students nested in 160 schools. The outcome variable of interest is the student-level (level 1) math achievement score (mathach). The variable ses is the socio-economic status of a student and therefore is at the student level. The variable meanses is the group-mean centered version of ses and therefore is at the school level (level 2). The variablesector is an indicator variable indicating if a school is public or catholic and is therefore a school-level variable. There are 90 public schools (sector=0) and 70 catholic schools (sector=1) in the sample.
The file that we are going to use is located in Chapter 2 in the Examples folder in your HLM folder and is called hsb1.sav and hsb2.sav (C:Program FilesHLM6ExamplesChapter2hsb1.sav and
C:Program FilesHLM6ExamplesChapter2hsb2.sav).
A brief word about sample sizes
The sample size necessary for multilevel modeling depends on several factors, including the number of parameters being estimated, the intraclass correlation, how balanced the data are, and some other things. In general, however, multilevel modeling is a large sample procedure. In particular, you usually want to have as many level 2 units as possible. Having lots of level 1 units can be helpful, but remember that level 1 units are correlated within each level 2 unit (the intraclass correlation), so increasing the number of level 1 units can become a case of diminishing returns. Level 2 units are independent (in a two level model), so by increasing the number of level 2 units, you are adding additional pieces of independent information to the data set. The validity of inferences made from small sample sizes is discussed in Hierarchical Linear Models by Raudenbush and Bryk on pages 280-284. Information regarding samples sizes can also be found in Snijders and Bosker's Multilevel Analysis. Some of the references listed at the end of this page also contain information regarding sample sizes.
Model building
At this point, we will focus on modeling building using HLM. We will pretend that we have already done data cleaning and have created all necessary variables. We will also assume that we have successfully gotten our data into HLM. For each of the models that we create, we will show both the model to be estimated in both the multi-equation and the single (mixed) equation format. The multi-equation format is shown by default; you can see the mixed equation by clicking on the mixed button in the lower left corner of the HLM interface.
Model 1: Unconditional means model
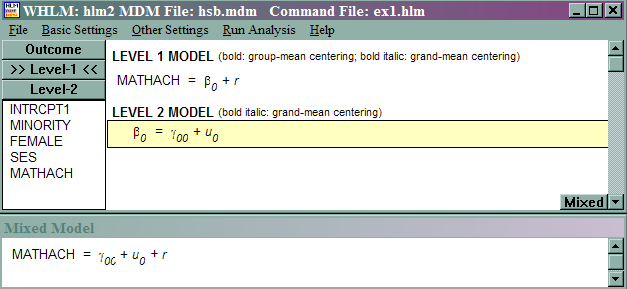
This model is referred as a one-way random effect ANOVA and is the simplest possible random effect linear model. The motivation for this model is the question of how much schools vary in their mean mathematics achievement. In terms of equations, we have the following, where rij ~ N(0, σ2) and u0j ~ N(0, τ2),
mathachij = β0j + rij
β0j = γ00 + u0j
SPECIFICATIONS FOR THIS HLM2 RUN Problem Title: no title The data source for this run = hsb.mdm The command file for this run = C:Datadataex1.hlm Output file name = c:hlm2.txt The maximum number of level-1 units = 7185 The maximum number of level-2 units = 160 The maximum number of iterations = 100 Method of estimation: restricted maximum likelihood Weighting Specification ----------------------- Weight Variable Weighting? Name Normalized? Level 1 no Level 2 no Precision no The outcome variable is mathach The model specified for the fixed effects was: ---------------------------------------------------- Level-1 Level-2 Coefficients Predictors ---------------------- --------------- intrcpt1, B0 INTRCPT2, G00 The model specified for the covariance components was: --------------------------------------------------------- Sigma squared (constant across level-2 units) Tau dimensions intrcpt1 Summary of the model specified (in equation format) --------------------------------------------------- Level-1 Model Y = B0 + R Level-2 Model B0 = G00 + U0 Iterations stopped due to small change in likelihood function ******* ITERATION 4 ******* Sigma_squared = 39.14831 Tau intrcpt1,B0 8.61431 Tau (as correlations) intrcpt1,B0 1.000 ---------------------------------------------------- Random level-1 coefficient Reliability estimate ---------------------------------------------------- intrcpt1, B0 0.901 ---------------------------------------------------- The value of the likelihood function at iteration 4 = -2.355840E+004 The outcome variable is mathach Final estimation of fixed effects: ---------------------------------------------------------------------------- Standard Approx. Fixed Effect Coefficient Error T-ratio d.f. P-value ---------------------------------------------------------------------------- For intrcpt1, B0 INTRCPT2, G00 12.636972 0.244412 51.704 159 0.000 ---------------------------------------------------------------------------- The outcome variable is mathach Final estimation of fixed effects (with robust standard errors) ---------------------------------------------------------------------------- Standard Approx. Fixed Effect Coefficient Error T-ratio d.f. P-value ---------------------------------------------------------------------------- For intrcpt1, B0 INTRCPT2, G00 12.636972 0.243628 51.870 159 0.000 ---------------------------------------------------------------------------- Final estimation of variance components: ----------------------------------------------------------------------------- Random Effect Standard Variance df Chi-square P-value Deviation Component ----------------------------------------------------------------------------- intrcpt1, U0 2.93501 8.61431 159 1660.23259 0.000 level-1, R 6.25686 39.14831 ----------------------------------------------------------------------------- Statistics for current covariance components model -------------------------------------------------- Deviance = 47116.793477 Number of estimated parameters = 2
Notes:
- The model we fit was
mathachij = β0j + rij
β0j = γ00 + u0jFilling in the parameter estimates we get
mathachij = β0j + rij
β0j = 12.64 + u0j
V(u0j) = 8.61
V(rij ) = 39.15
- The estimated between variance, τ2, corresponds to the term intrcpt1 in the output of final estimation of variance components and the estimated within variance, σ2, corresponds to the term level-1 in the same output section. For this model, τ2 is 8.61 and σ2 is 39.15.
- Based on the covariance estimates, we can compute the intraclass correlation: 8.61431/(8.61431 + 39.14831) = .18. This tells us the portion of the total variance that occurs between schools.
- To measure the magnitude of the variation among schools in their mean achievement levels, we can calculate the plausible values range for these means, based on the between variance we obtained from the model: 12.64 ± 1.96*(8.61)1/2 = (6.89, 18.39).
- The reliability of the random effect of the level 1 intercept is the average reliability of the level 2 units. It measures the overall reliability of the OLS estimates for each of the intercepts. The reliability estimate for this model is .901.
Model 2: Including effects of school level (level 2) predictors – predicting mathach from meanses
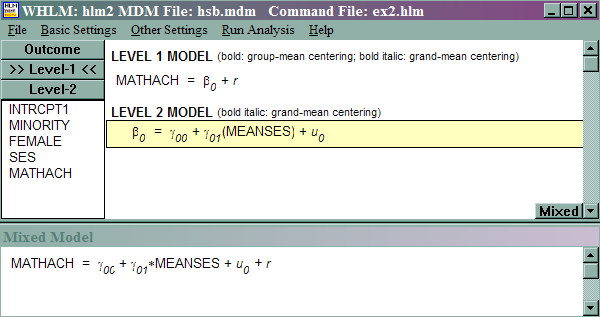
This model is referred to as regression with means-as-outcomes by Raudenbush and Bryk. This model is motivated by the question of whether schools with high meanses also have high math achievement. In other words, we want to understand why there is a school difference with regard to mathematics achievement. In terms of regression equations, we have the following:
mathachij = β0j + rij
β0j = γ00 + γ01(meanses) + u0j
SPECIFICATIONS FOR THIS HLM2 RUN Problem Title: no title The data source for this run = hsb.mdm The command file for this run = C:Datadataex2.hlm Output file name = c:hlm2.txt The maximum number of level-1 units = 7185 The maximum number of level-2 units = 160 The maximum number of iterations = 100 Method of estimation: restricted maximum likelihood Weighting Specification ----------------------- Weight Variable Weighting? Name Normalized? Level 1 no Level 2 no Precision no The outcome variable is mathach The model specified for the fixed effects was: ---------------------------------------------------- Level-1 Level-2 Coefficients Predictors ---------------------- --------------- intrcpt1, B0 INTRCPT2, G00 meanses, G01 The model specified for the covariance components was: --------------------------------------------------------- Sigma squared (constant across level-2 units) Tau dimensions intrcpt1 Summary of the model specified (in equation format) --------------------------------------------------- Level-1 Model Y = B0 + R Level-2 Model B0 = G00 + G01*(meanses) + U0 Iterations stopped due to small change in likelihood function ******* ITERATION 6 ******* Sigma_squared = 39.15708 Tau intrcpt1,B0 2.63870 Tau (as correlations) intrcpt1,B0 1.000 ---------------------------------------------------- Random level-1 coefficient Reliability estimate ---------------------------------------------------- intrcpt1, B0 0.740 ---------------------------------------------------- The value of the likelihood function at iteration 6 = -2.347972E+004 The outcome variable is mathach Final estimation of fixed effects: ---------------------------------------------------------------------------- Standard Approx. Fixed Effect Coefficient Error T-ratio d.f. P-value ---------------------------------------------------------------------------- For intrcpt1, B0 INTRCPT2, G00 12.649436 0.149280 84.736 158 0.000 meanses, G01 5.863538 0.361457 16.222 158 0.000 ---------------------------------------------------------------------------- The outcome variable is mathach Final estimation of fixed effects (with robust standard errors) ---------------------------------------------------------------------------- Standard Approx. Fixed Effect Coefficient Error T-ratio d.f. P-value ---------------------------------------------------------------------------- For intrcpt1, B0 INTRCPT2, G00 12.649436 0.148377 85.252 158 0.000 meanses, G01 5.863538 0.320211 18.311 158 0.000 ---------------------------------------------------------------------------- Final estimation of variance components: ----------------------------------------------------------------------------- Random Effect Standard Variance df Chi-square P-value Deviation Component ----------------------------------------------------------------------------- intrcpt1, U0 1.62441 2.63870 158 633.51744 0.000 level-1, R 6.25756 39.15708 ----------------------------------------------------------------------------- Statistics for current covariance components model -------------------------------------------------- Deviance = 46959.446959 Number of estimated parameters = 2
Notes:
- The model we fit was
mathachij = β0j + rij
β0j = γ00 + γ01(meanses) + u0jFilling in the parameter estimates we get
mathachij = β0j + rij
β0j = 12.65 +5.86(meanses) + u0j
V(u0j) = 2.64
V(rij ) = 39.16
- In a single equation our model will be written as: mathachij = γ00 + γ01(meanses) + u0j + rij .
- The coefficient for the constant is the predicted math achievement when all predictors are 0; hence, when the average school SES is 0, the students' math achievement is predicted to be 12.65.
- A range of plausible values for school means, given that all schools have meanses of zero, is 12.65 ± 1.96 *(2.64)1/2 = (9.47, 15.83).
- The variance component representing variation between schools decreases greatly (from 8.61 to 2.64). This indicates that the level-2 variable meanses explains a large portion of the school-to-school variation in mean math achievement. More precisely, the proportion of variance explained by meanses is (8.61 – 2.64)/8.61 = .69, that is about 69% of the explainable variation in school mean math achievement scores can be explained by meanses.
- Do school achievement means still vary significantly once meanses is controlled? The output of final estimation of variance components gives the test for the variance component for the intrcpt1 to be zero with chi-square of 633.52 with 158 degrees of freedom. This is statistically significant. Therefore, we conclude that after controlling for meanses, significant variation among school mean math achievement still remains to be explained.
- We can also calculate the conditional intraclass correlation conditional on the values of meanses: 2.64/(2.64 + 39.16) = .06 measures the degree of dependence among observations within schools that are of the same meanses.
Model 3: Including effects of student-level predictors-predicting mathach from group–centered student-level ses
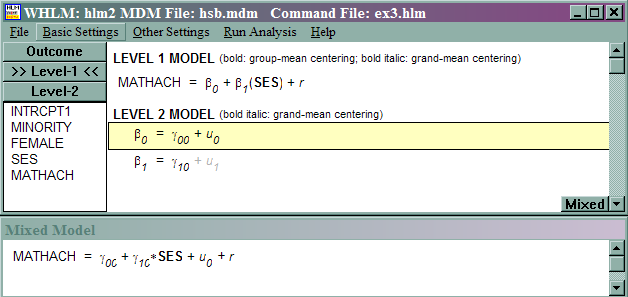
This model is referred to as a random-coefficient model by Raudenbush and Bryk. Pretend that we run a regression of mathach on group-centered ses for each school; in other words, we would run 160 regressions.
- What would be the average of the 160 regression equations (both intercept and slope)?
- How much do the regression equations vary from school to school?
- What is the correlation between the intercepts and slopes?
These are some of the questions that motivates the following model.
mathachij = β0j + β1j (SES – meanses) + rij
β0j = γ00 + u0j
β1j = γ10 + u1j
Sigma_squared = 36.70356
Tau intrcpt1,B0 8.68087 0.04701 SES,B1 0.04701 0.68038
Tau (as correlations) intrcpt1,B0 1.000 0.019 SES,B1 0.019 1.000
---------------------------------------------------- Random level-1 coefficient Reliability estimate ---------------------------------------------------- intrcpt1, B0 0.908 SES, B1 0.260 ----------------------------------------------------
The value of the likelihood function at iteration 18 = -2.335620E+004
Final estimation of fixed effects: ---------------------------------------------------------------------------- Standard Approx. Fixed Effect Coefficient Error T-ratio d.f. P-value ---------------------------------------------------------------------------- For intrcpt1, B0 INTRCPT2, G00 12.636197 0.244503 51.681 159 0.000 For SES slope, B1 INTRCPT2, G10 2.193157 0.127879 17.150 159 0.000 ----------------------------------------------------------------------------
Final estimation of fixed effects (with robust standard errors) ---------------------------------------------------------------------------- Standard Approx. Fixed Effect Coefficient Error T-ratio d.f. P-value ---------------------------------------------------------------------------- For intrcpt1, B0 INTRCPT2, G00 12.636197 0.243738 51.843 159 0.000 For SES slope, B1 INTRCPT2, G10 2.193157 0.127846 17.155 159 0.000 ----------------------------------------------------------------------------
Final estimation of variance components: ----------------------------------------------------------------------------- Random Effect Standard Variance df Chi-square P-value Deviation Component ----------------------------------------------------------------------------- intrcpt1, U0 2.94633 8.68087 159 1770.85120 0.000 SES slope, U1 0.82485 0.68038 159 213.43769 0.003 level-1, R 6.05835 36.70356 -----------------------------------------------------------------------------
Statistics for current covariance components model -------------------------------------------------- Deviance = 46712.398925 Number of estimated parameters = 4
Notes:
- The model we fit was
mathachij = β0j + β1j (SES – meanses) + rij
β0j = γ00 + u0j
β1j = γ10 + u1jFilling in the parameter estimates we get
mathachij = β0j + β1j (SES – meanses) + rij
β0j = 12.64 + u0j
β1j = 2.19 + u1j
V(u0j) = 8.68
V(u1j) = .68
V(rij ) = 36.7
- In a single equation our model would be written as:
mathachij = γ00 + u0j + (γ10 + u1j )(SES – meanses) + rij
= γ00 + γ10 *(SES – meanses) + u0j + u1j *(SES – meanses) + rij
- The estimate for the variance of the slope for group-centered SES is 0.68. The p-value is .003. Because the test is statistically significant, we reject the hypothesis that there is no difference in slopes among schools.
- The 95% plausible value range for the school means is 12.64 ± 1.96 *(8.68)1/2 = (6.87, 18.41).
- The 95% plausible value range for the SES-achievement slope is 2.19 ± 1.96 *(.68)1/2 = (.57, 3.81).
- Notice that the residual variance is now 36.70, compared to the residual variance of 39.15 in the one-way ANOVA with random effects (unconditional means) model. We can compute the proportion variance explained at level 1 as (39.15 – 36.70) / 39.15 = .063. This suggests using student-level SES as a predictor of math achievement reduced the within-school variance by 6.3%.
- The correlation between the intercept and the slope is .019. It seems that they are not highly correlated.
Model 4: Including both level-1 and level-2 predictors -predicting mathach from meanses, sector, cses and the cross level interaction of meanses and sector with cses
This model is referred to as an intercepts- and slopes-as-outcomes model by Raudenbush and Bryk. We have examined the variability of the regression equations across schools. Now we will build an explanatory model to account for the variability. We want to model the following:
mathachij = β0j + β1j (SES – meanses) + rij
β0j = γ00 + γ01(sector) + γ02(meanses) + u0j
β1j = γ10 + γ11(sector) + γ12(meanses) + u1j

SPECIFICATIONS FOR THIS HLM2 RUN Problem Title: no title The data source for this run = hsb.mdm The command file for this run = C:Datadataex4.hlm Output file name = c:hlm2.txt The maximum number of level-1 units = 7185 The maximum number of level-2 units = 160 The maximum number of iterations = 100 Method of estimation: restricted maximum likelihood Weighting Specification ----------------------- Weight Variable Weighting? Name Normalized? Level 1 no Level 2 no Precision no The outcome variable is mathach The model specified for the fixed effects was: ---------------------------------------------------- Level-1 Level-2 Coefficients Predictors ---------------------- --------------- intrcpt1, B0 INTRCPT2, G00 SECTOR, G01 meanses, G02 * SES slope, B1 INTRCPT2, G10 SECTOR, G11 meanses, G12 '*' - This level-1 predictor has been centered around its group mean. The model specified for the covariance components was: --------------------------------------------------------- Sigma squared (constant across level-2 units) Tau dimensions intrcpt1 SES slope Summary of the model specified (in equation format) --------------------------------------------------- Level-1 Model Y = B0 + B1*(SES) + R Level-2 Model B0 = G00 + G01*(SECTOR) + G02*(meanses) + U0 B1 = G10 + G11*(SECTOR) + G12*(meanses) + U1 Iterations stopped due to small change in likelihood function ******* ITERATION 61 ******* Sigma_squared = 36.70313 Tau intrcpt1,B0 2.37996 0.19058 SES,B1 0.19058 0.14892 Tau (as correlations) intrcpt1,B0 1.000 0.320 SES,B1 0.320 1.000 ---------------------------------------------------- Random level-1 coefficient Reliability estimate ---------------------------------------------------- intrcpt1, B0 0.733 SES, B1 0.073 ---------------------------------------------------- The value of the likelihood function at iteration 61 = -2.325094E+004 The outcome variable is mathach Final estimation of fixed effects: ---------------------------------------------------------------------------- Standard Approx. Fixed Effect Coefficient Error T-ratio d.f. P-value ---------------------------------------------------------------------------- For intrcpt1, B0 INTRCPT2, G00 12.096006 0.198734 60.865 157 0.000 SECTOR, G01 1.226384 0.306272 4.004 157 0.000 meanses, G02 5.333056 0.369161 14.446 157 0.000 For SES slope, B1 INTRCPT2, G10 2.937981 0.157135 18.697 157 0.000 SECTOR, G11 -1.640954 0.242905 -6.756 157 0.000 meanses, G12 1.034427 0.302566 3.419 157 0.001 ---------------------------------------------------------------------------- The outcome variable is mathach Final estimation of fixed effects (with robust standard errors) ---------------------------------------------------------------------------- Standard Approx. Fixed Effect Coefficient Error T-ratio d.f. P-value ---------------------------------------------------------------------------- For intrcpt1, B0 INTRCPT2, G00 12.096006 0.173699 69.638 157 0.000 SECTOR, G01 1.226384 0.308484 3.976 157 0.000 meanses, G02 5.333056 0.334600 15.939 157 0.000 For SES slope, B1 INTRCPT2, G10 2.937981 0.147620 19.902 157 0.000 SECTOR, G11 -1.640954 0.237401 -6.912 157 0.000 meanses, G12 1.034427 0.332785 3.108 157 0.003 ---------------------------------------------------------------------------- Final estimation of variance components: ----------------------------------------------------------------------------- Random Effect Standard Variance df Chi-square P-value Deviation Component ----------------------------------------------------------------------------- intrcpt1, U0 1.54271 2.37996 157 605.29503 0.000 SES slope, U1 0.38590 0.14892 157 162.30867 0.369 level-1, R 6.05831 36.70313 ----------------------------------------------------------------------------- Statistics for current covariance components model -------------------------------------------------- Deviance = 46501.875643 Number of estimated parameters = 4
Notes:
- The model we fit was
mathachij = β0j + β1j (ses – meanses) + rij
β0j = γ00 + γ01(sector) + γ02(meanses) + u0j
β1j = γ10 + γ11(sector) + γ12(meanses) + u1jFilling in the parameter estimates we get
mathachij = β0j + β1j (ses – meanses) + rij
β0j = 12.10 + 1.22(sector) + 5.33(meanses) + u0j
β1j = 2.94 + -1.64(sector) + 1.03(meanses) + u1jV(u0j) = 2.37
V(u1j) = .15
V(rij ) = 36.7
- In a single equation our model will be written as:
mathachij = γ00 + γ01(meanses) + γ02(sector) + u0j
+ (γ10 + γ11(meanses) + γ12(sector) + u1j)* (ses – meanses) + rij
= γ00 + γ01(meanses) + γ02(sector)
+ γ10*(ses-meanses) + γ11*meanses*(ses-meanses) + γ12*sector*(ses-meanses)
+ u0j + u1j* (SES – meanses) + rij - The estimate for the variance of the ses slope is .15 with p-value .369; hence, we fail to reject the null hypothesis that there is no significant variation among the slopes of ses. We may want to use a simpler model where the slope of ses varies nonrandomly with respect to the level-2 variables meanses and sector.
- The correlation between the level-1 intercept and the slope for ses is given as .32 from the earlier part of the output.
Graphing the results
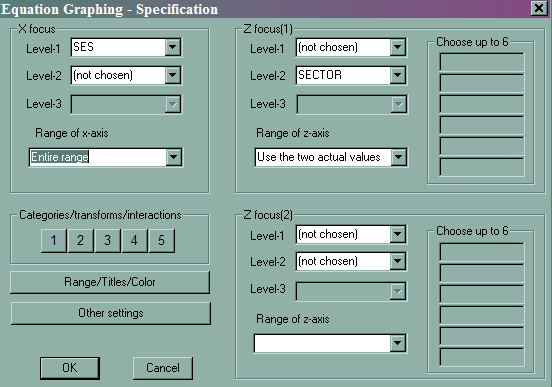
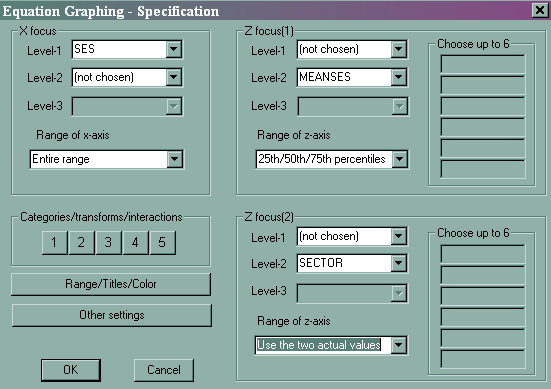
HLM has some nice features to help you visualize the effect of level 2 variables. After running the model, you can click on File, and then Graph Equations and then Model Graphs. All of the graphs in this section are based on the last model that we ran, which we called model 4.
- File -> Graph Equations -> Model Graphs
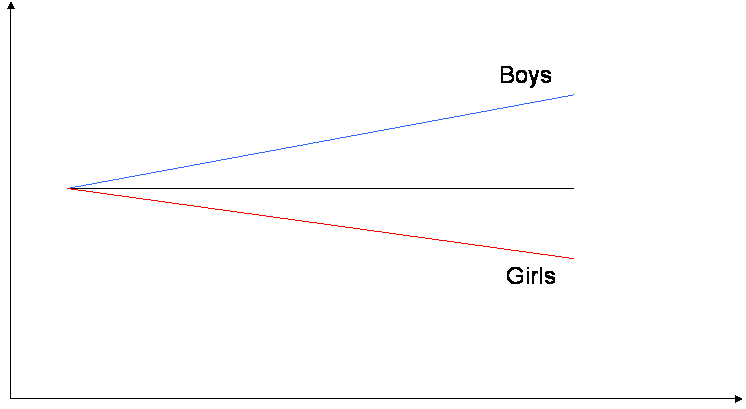
- Slope of ses by sector
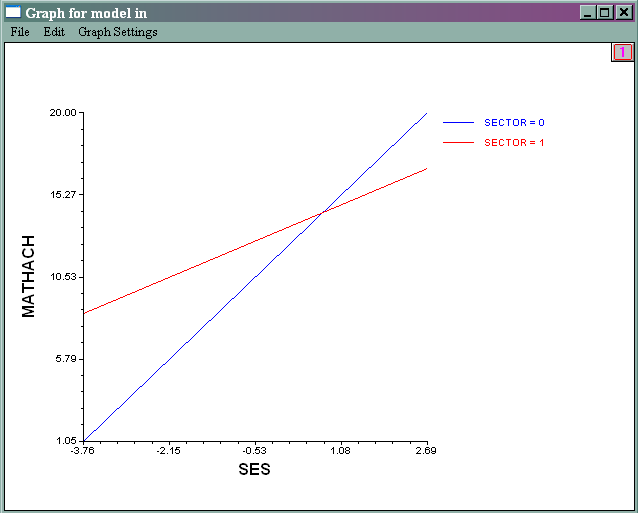
- File -> Graph Equations -> Model Graphs
- Slope of SES by different meanses
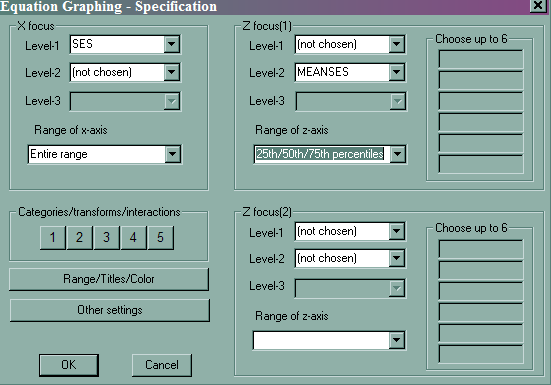
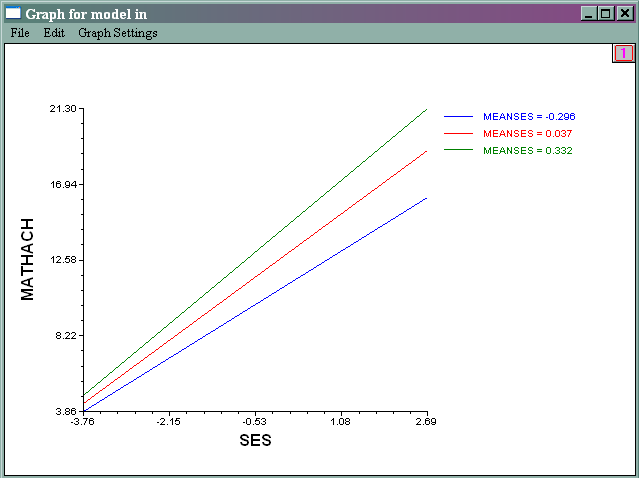
- File -> Graph Equations -> Model Graphs
- Putting the two plots together
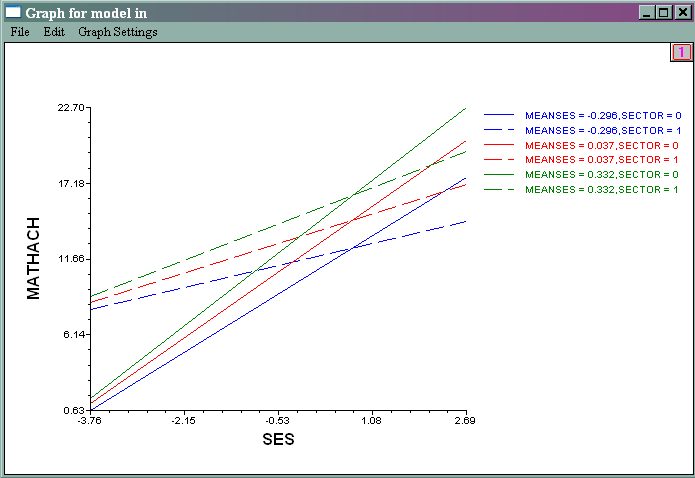
Model fit
- Model checking based on the residual file
- Testing homogeneity of level-1 variances
- Multivariate hypothesis tests on fixed effects
- Multivariate tests of variance-covariance components specification
Residual file and analysis of model fit
Let's say that our final model is going to be based on the last model we ran with both the intercept and the slope for ses as random effects. What about the model fit? Are there any potential problems with the model?
- Any outliers or influential observations?
- Any omitted variables?
- Normality at each level?
- Homogeneity of level-1 variances?
1. Residual file
We can make use of the residual file that HLM creates to check model fit. This time before running the model, we will request that a file of residuals be created. From the Basic Settings, click on Level-2 Residual File and the following dialog window will be displayed. We can choose to include in the file extra level-2 variables that are not in the model, and we can also choose the residual file type. We will include variables in addition to our two level-2 variables in the residual file, and we will request that the residual file be created in SPSS format. All the plots and analyses based on the residual file will be preformed in SPSS. You need to rerun the model after you specify what you want in the residual file. You can include a path specification along with the file name.

Let's have a look at the residual file for our model. The last six variables are all the level-2 variables in the file, and we have requested to have them in the residual file. Each observation corresponds to a level-2 unit. In our case, there will be 160 observations in the residual file, because there are 160 schools.
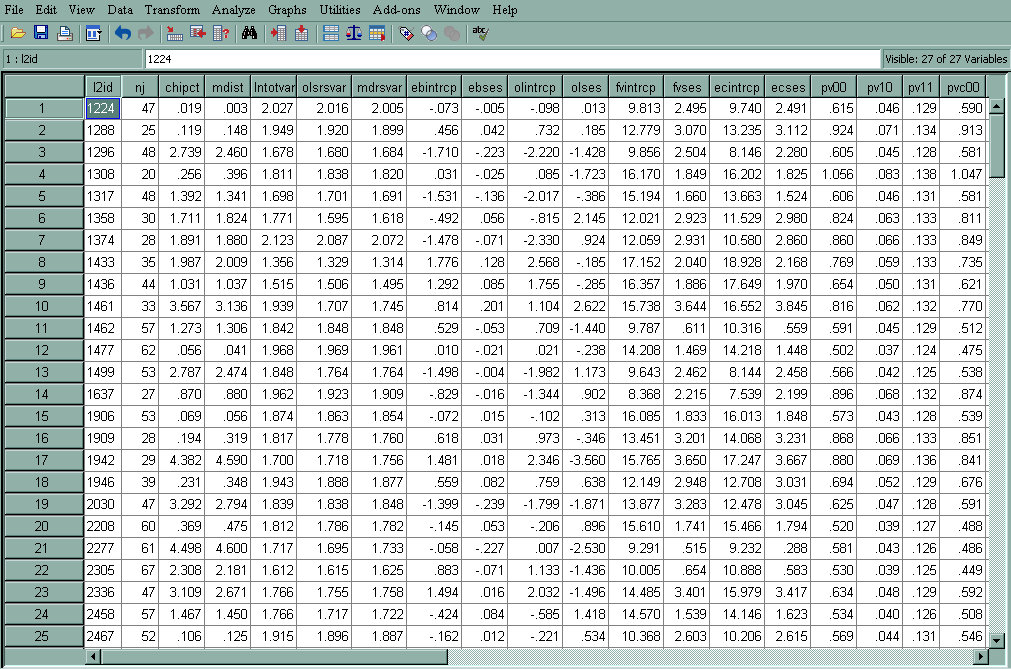
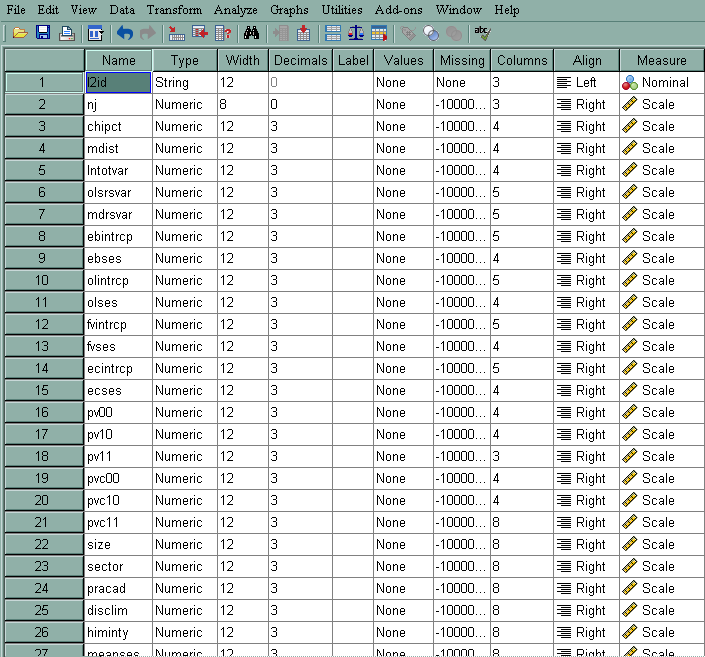
- l2id – Level-2 identification variable
- nj – Size of the current level-2 unit
- chipct – Theoretical values from a χ2 (v) with v being the number of random factors and this variable is paired with mdist to produce a Q-Q plot
- mdist – Mahalanobis distance; under the normality assumption, it should be approximately χ2 (v) with v being the number of random factors. It provides a summary measure of the distance of the empirical Bayes estimates of the fixed effect parameters from their "fitted value" given by our defining equations.
- lntotvar – Natural log of the total dispersion within each level-2 unit
- olsrsvar – Natural log of the residual dispersion within each level-2 unit based on its OLS estimate
- mdrsvar – Natural log of the residual standard deviation from the final fitted fixed effect model
- ebintrcp – Empirical Bayes residual for the intercept, u0j
- ebses – Empirical Bayes residual for the slope of SES, u1j
- olintrcp – Ordinary least square residual for the intercept, only for the units with enough data
- olses – Ordinary least square residual for the slope of SES, only for the units with enough data
- fvintrcp – Fitted value for the intercept based on its level-2 estimators, β0j. For example, for school id 1224, it is equal to12.096006 + 1.226384* 0 + 5.333056*(-.428) = 9.814
- fvses – Fitted value for the slope of SES based on its level-2 estimators, β1j
- pv00 – Posterior variance of the empirical Bayes estimate for the intercept
- pv10 – Posterior covariance of the empirical Bayes estimate for the intercept and SES
- pv11 – Posterior variance of the empirical Bayes estimate for the slope
- pvc00 – Posterior variance of the coefficient for the random intercept
- pvc10 – Posterior covariance of the coefficients for the random intercept and random slope
- pvc11 – Posterior variance of the coefficient for the random slope
- size – Level 2 predictor variable from the original data file
- pracad – Level 2 predictor variable from the original data file
- disclim – Level 2 predictor variable from the original data file
- himinity – Level 2 predictor variable from the original data file
- sector – Level 2 predictor variable from the original data file
- meanses – Level 2 predictor variable from the original data file
Q-Q Plot of chipct against mdist (Scatterplot of chipct against mdist)
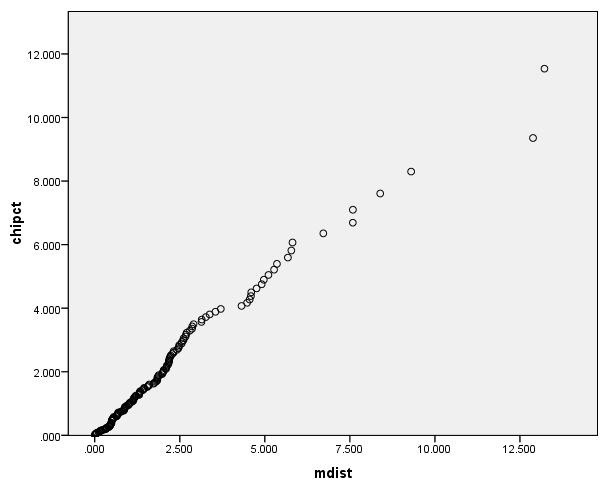
Under the assumption of normality at level-2, the plot of chipct against mdist should be a 45 degree line. Otherwise, we have some evidence against the normality assumption. For example, in our plot we see some deviation from the normality at the right end of the plot. The plot shows us that there may be some outliers that need further investigation.
Histogram of mdrsvar
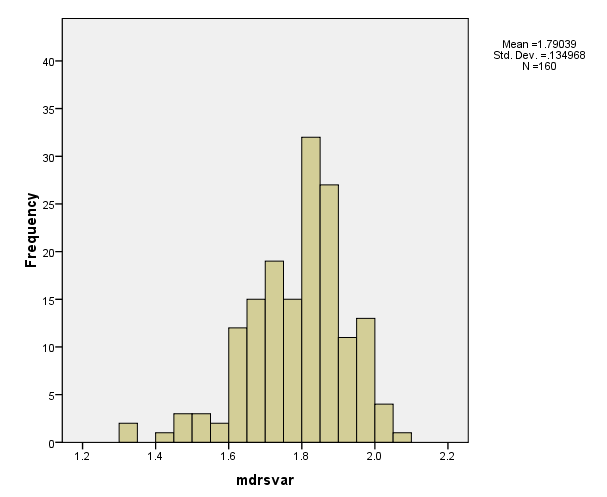
The variable mdrsvar (the natural log of the residual standard deviation from the final fitted fixed effect model) measures the within-school standard deviation for the 160 schools based on the final fitted model. From the histogram we see that there are a few schools that have smaller within-school variance than others.
Q-Q Plot of standardized mdrsvar
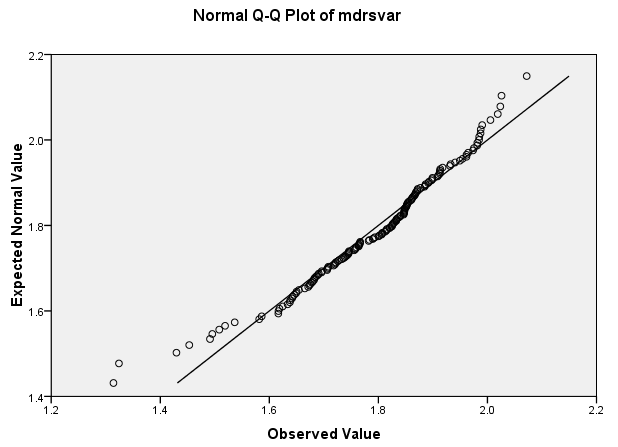
The purpose of this plot is similar to the previous one. If the data are normally distributed, the dots will fall along the line. The dots towards the left and right of the graph fall away from the line, indicating that there is some divergence from normality in the tails of the distribution.
Potential level-2 predictors
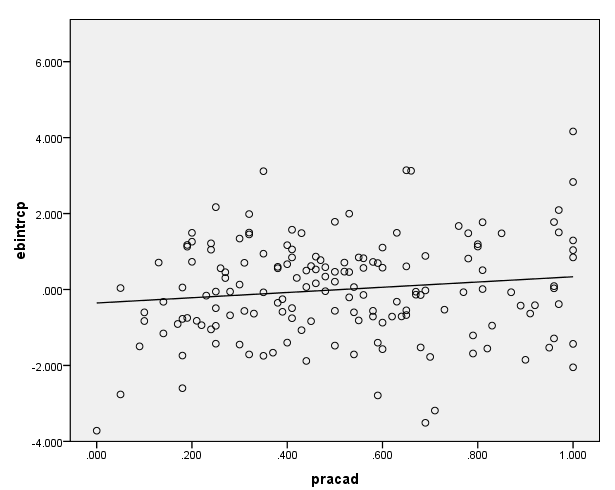
Potentially, there are other level-2 variables that should be included in the model. (These other variables may or may not be in your data set.) For example, the variable pracad, the proportion of students in the academic track, may be a good candidate as a level-2 variable. To help visualize this, we can plot the empirical Bayes residual estimate for the intercept for each school against pracad. The evidence that there is not much of an association between the intercept and pracad suggests that this variable should not be included in the model unless there is good theoretical reason to include it. All the same, we may have a model specification error, meaning we have omitted one or more important variables.
Nonlinearity at level-2
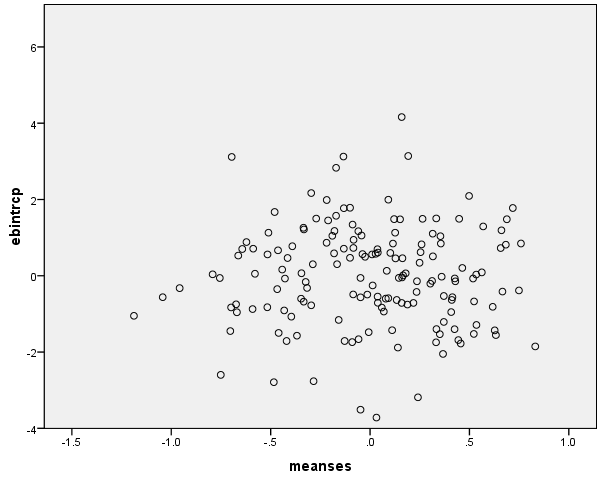
This is very similar to what we usually do in an OLS analysis. We plot the residual against a continuous predictor to detect any nonlinearity. In this case, we have the residual for the intercept against the level-2 predictor meanses. A curved plot will show evidence of nonlinearity. We don't seem to have much of a problem with nonlinearity here.
2. Testing the homogeneity of level-1 variances
To test the homogeneity of the level 1 variance we will choose Other Settings and then Hypothesis Testing. We will then check the box in the lower left corner to get the test of homogeneity of level 1 variance as shown below, i.e., a test that the variance of mathach is the same across schools.
The test below suggests that the variance of mathach varies significantly across schools, contrary to the assumption of homogeneity of the level-1 variance. If the variance of matchach is related to level 1 or level 2 predictors, this can bias the estimates (see Raudenbush and Bryk, pages. 263-267 for more information). After making the above selection, rerun the model and look at the very bottom of the output for this table.
Test of homogeneity of level-1 variance ---------------------------------------- Chi-square statistic = 245.76576 Number of degrees of freedom = 159 P-value = 0.000
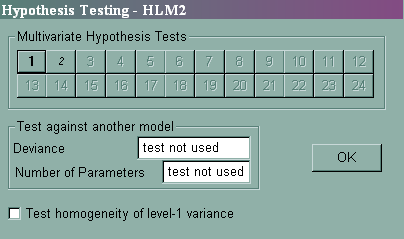
3. Multivariate hypothesis tests for fixed effects
To test the effect of sector on the intercept and on the ses slope simultaneously we will choose Hypothesis Testing from the Other Settings pull-down menu. We will then click on the 1 button to specify our first hypothesis (see below).
We then fill out the boxes below to indicate we wish to jointly test γ01 = 0 and γ11 = 0 .
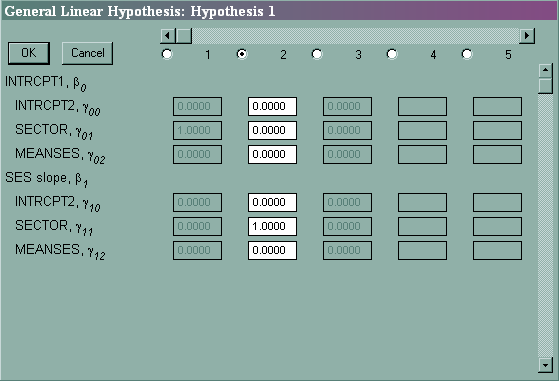
After specifying your hypothesis test(s) and clicking on OK and OK, rerun the model and look towards the bottom of the output.
---------------------------------------------------------------------------- Results of General Linear Hypothesis Testing ----------------------------------------------------------------------------- Coefficients Contrast ----------------------------------------------------------------------------- For INTRCPT1, B0 INTRCPT2, G00 12.096006 0.000 0.000 SECTOR, G01 1.226384 1.000 0.000 MEANSES, G02 5.333056 0.000 0.000 For SES slope, B1 INTRCPT2, G10 2.937981 0.000 0.000 SECTOR, G11 -1.640954 0.000 1.000 MEANSES, G12 1.034427 0.000 0.000 Chi-square statistic = 60.596880 Degrees of freedom = 2 P-value = 0.000000
4. Multivariate tests of variance-covariance components specification
From Model 4 that we ran before, we saw that the p-value for the test of the variance component of the slope is not significant. This suggests that we may not want to model the slope as randomly varying. A simpler model would be that the slope of the variable ses varies nonrandomly for the level-2 variables sector and meanses. We may want to compare these two models to decide if the simpler model is comparable with the previous one.
- REML (restricted maximum likelihood) versus FML (full maximum likelihood)
- REML and FML will usually produce similar results for the level-1 residual (σ2), but there can be noticeable differences for the variance-covariance matrix of the random effects.
- REML is the default estimation method in HLM.
- If the number of level-2 units is large, then the difference will be small.
- If the number of level-2 units is small, then FML variance estimates will be smaller than REML, leading to artificially short confidence interval and problematic significant tests.
- Nested models
- If the fixed effects are the same, and there are fewer random effects in the reduced model, then both REML or FML are fine.
- If one model has fewer fixed effects and possibly fewer random effects, then use FML to compare models.
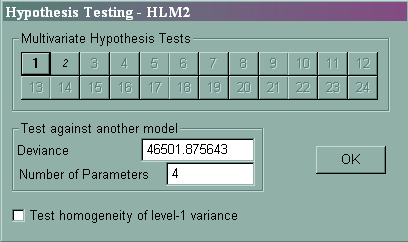
Sigma_squared = 36.76611
Tau intrcpt1,B0 2.37524
Tau (as correlations) intrcpt1,B0 1.000
---------------------------------------------------- Random level-1 coefficient Reliability estimate ---------------------------------------------------- intrcpt1, B0 0.732 ----------------------------------------------------
The value of the likelihood function at iteration 6 = -2.325148E+004 Final estimation of fixed effects: ---------------------------------------------------------------------------- Standard Approx. Fixed Effect Coefficient Error T-ratio d.f. P-value ---------------------------------------------------------------------------- For intrcpt1, B0 INTRCPT2, G00 12.096251 0.198643 60.894 157 0.000 SECTOR, G01 1.224401 0.306117 4.000 157 0.000 meanses, G02 5.336698 0.368978 14.463 157 0.000 For SES slope, B1 INTRCPT2, G10 2.935860 0.150705 19.481 7179 0.000 SECTOR, G11 -1.642102 0.233097 -7.045 7179 0.000 meanses, G12 1.044120 0.291042 3.588 7179 0.001 ----------------------------------------------------------------------------
Final estimation of fixed effects (with robust standard errors) ---------------------------------------------------------------------------- Standard Approx. Fixed Effect Coefficient Error T-ratio d.f. P-value ---------------------------------------------------------------------------- For intrcpt1, B0 INTRCPT2, G00 12.096251 0.173691 69.642 157 0.000 SECTOR, G01 1.224401 0.308507 3.969 157 0.000 meanses, G02 5.336698 0.334617 15.949 157 0.000 For SES slope, B1 INTRCPT2, G10 2.935860 0.147580 19.893 7179 0.000 SECTOR, G11 -1.642102 0.237223 -6.922 7179 0.000 meanses, G12 1.044120 0.332897 3.136 7179 0.002 ----------------------------------------------------------------------------
Final estimation of variance components: ----------------------------------------------------------------------------- Random Effect Standard Variance df Chi-square P-value Deviation Component ----------------------------------------------------------------------------- intrcpt1, U0 1.54118 2.37524 157 604.29893 0.000 level-1, R 6.06351 36.76611 -----------------------------------------------------------------------------
Statistics for current covariance components model -------------------------------------------------- Deviance = 46502.952734 Number of estimated parameters = 2
Variance-Covariance components test ----------------------------------- Chi-square statistic = 1.07710 Number of degrees of freedom = 2 P-value = >.500
Other issues
- Modeling heterogeneity of level-1 variances
- Models without a level-1 intercept
- Constraints of fixed effects
- Level-1 variable as a random effect but not a fixed effect
- Testing multi-degree-of-freedom variables
- Using sampling weights
- Using multiply imputed data
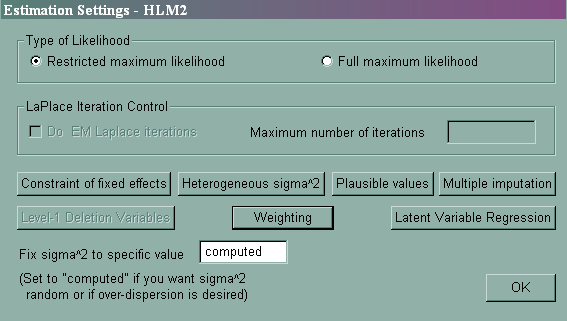
1. Modeling heterogeneity of level-1 variances
Sometimes, the level-1 variance may be heterogeneous. For example, we may expect that female students and male students have different variances. Thus, we want to model the level-1 variance to be a function of the variable female. From pull-down menu Other Settings, we can choose Estimation Settings, and then Heterogeneous sigma^2. We then have a choice on which variable(s) to choose to model the heterogeneity. Here we picked the variable female. Click on OK and then OK, and rerun the model. From the output of Summary of Model Fit, we see that the model with heterogeneous sigma^2 is a better model (with p-value much less than .05).


RESULTS FOR HETEROGENEOUS SIGMA-SQUARED (macro iteration 4) Var(R) = Sigma_squared and log(Sigma_squared) = alpha0 + alpha1(FEMALE) Model for level-1 variance -------------------------------------------------------------------- Standard Parameter Coefficient Error Z-ratio P-value -------------------------------------------------------------------- INTRCPT1 ,alpha0 3.66570 0.024718 148.301 0.000 FEMALE ,alpha1 -0.12106 0.033936 -3.567 0.001 -------------------------------------------------------------------- Summary of Model Fit ------------------------------------------------------------------- Model Number of Deviance Parameters ------------------------------------------------------------------- 1. Homogeneous sigma_squared 10 46494.59261 2. Heterogeneous sigma_squared 11 46482.09334 ------------------------------------------------------------------- Model Comparison Chi-square df P-value ------------------------------------------------------------------- Model 1 vs Model 2 12.49926 1 0.001 Tau INTRCPT1,B0 2.29090 0.18183 SES,B1 0.18183 0.06325 Tau (as correlations) INTRCPT1,B0 1.000 0.478 SES,B1 0.478 1.000 ---------------------------------------------------- Random level-1 coefficient Reliability estimate ---------------------------------------------------- INTRCPT1, B0 0.725 SES, B1 0.033 ---------------------------------------------------- The value of the likelihood function at iteration 2 = -2.324105E+004 The outcome variable is MATHACH Final estimation of fixed effects: ---------------------------------------------------------------------------- Standard Approx. Fixed Effect Coefficient Error T-ratio d.f. P-value ---------------------------------------------------------------------------- For INTRCPT1, B0 INTRCPT2, G00 12.059116 0.196011 61.523 157 0.000 SECTOR, G01 1.245117 0.301910 4.124 157 0.000 MEANSES, G02 5.326542 0.363835 14.640 157 0.000 For SES slope, B1 INTRCPT2, G10 2.952729 0.153406 19.248 157 0.000 SECTOR, G11 -1.644758 0.236725 -6.948 157 0.000 MEANSES, G12 1.032606 0.295125 3.499 157 0.001 ---------------------------------------------------------------------------- The outcome variable is MATHACH Final estimation of fixed effects (with robust standard errors) ---------------------------------------------------------------------------- Standard Approx. Fixed Effect Coefficient Error T-ratio d.f. P-value ---------------------------------------------------------------------------- For INTRCPT1, B0 INTRCPT2, G00 12.059116 0.173152 69.645 157 0.000 SECTOR, G01 1.245117 0.307648 4.047 157 0.000 MEANSES, G02 5.326542 0.333385 15.977 157 0.000 For SES slope, B1 INTRCPT2, G10 2.952729 0.148115 19.935 157 0.000 SECTOR, G11 -1.644758 0.239529 -6.867 157 0.000 MEANSES, G12 1.032606 0.336341 3.070 157 0.003 ---------------------------------------------------------------------------- Final estimation of variance components: ----------------------------------------------------------------------------- Random Effect Standard Variance df Chi-square P-value Deviation Component ----------------------------------------------------------------------------- INTRCPT1, U0 1.51357 2.29090 157 599.75645 0.000 SES slope, U1 0.25149 0.06325 157 162.54860 0.364 ----------------------------------------------------------------------------- Statistics for current covariance components model -------------------------------------------------- Deviance = 46482.093344 Number of estimated parameters = 11
Model comparison test ----------------------------------- Chi-square statistic = 19.78230 Number of degrees of freedom = 7 P-value = 0.006
2. Models without a level-1 intercept
Sometimes, we may want to exclude the intercept from our model. For example, we may have a level-1 categorical variable and we want to include all the categories of this variable in the model. To accomplish this, we have to exclude the intercept; otherwise, our model will be over-identified.


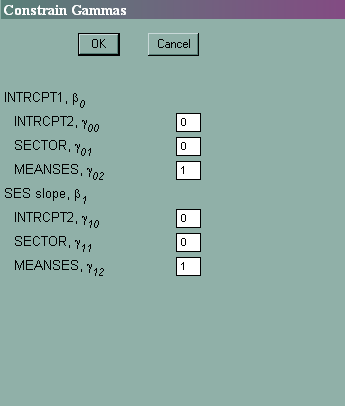
3. Constraints of fixed effects
Choose Other Settings then Estimation Settings, and then Constraint of fixed effects. From here, we can constrain, for example, the effect of γ02 to be equal to γ12.
Summary of the model specified (in equation format) --------------------------------------------------- Level-1 Model Y = B0 + B1*(SES) + R Level-2 Model B0 = G00 + G01*(SECTOR) + G02*(MEANSES) + U0 B1 = G10 + G11*(SECTOR) + G12*(MEANSES) + U1 02G = 12G Iterations stopped due to small change in likelihood function ******* ITERATION 19 ******* Sigma_squared = 36.75129 Standard Error of Sigma_squared = 0.62663 Tau INTRCPT1,B0 3.38650 -0.42733 SES,B1 -0.42733 0.36901 Standard Errors of Tau INTRCPT1,B0 0.47559 0.24733 SES,B1 0.24733 0.24605 Tau (as correlations) INTRCPT1,B0 1.000 -0.382 SES,B1 -0.382 1.000 ---------------------------------------------------- Random level-1 coefficient Reliability estimate ---------------------------------------------------- INTRCPT1, B0 0.795 SES, B1 0.162 ---------------------------------------------------- The value of the likelihood function at iteration 19 = -2.328375E+004 The outcome variable is MATHACH Final estimation of fixed effects: ---------------------------------------------------------------------------- Standard Approx. Fixed Effect Coefficient Error T-ratio d.f. P-value ---------------------------------------------------------------------------- For INTRCPT1, B0 INTRCPT2, G00 11.741607 0.222122 52.861 157 0.000 SECTOR, G01 2.016592 0.335380 6.013 157 0.000 MEANSES, G02 * 2.654259 0.237376 11.182 157 0.000 For SES slope, B1 INTRCPT2, G10 3.159636 0.163404 19.336 158 0.000 SECTOR, G11 -2.096300 0.249567 -8.400 158 0.000 ---------------------------------------------------------------------------- The "*" gammas have been constrained. See the table on the header page. The outcome variable is MATHACH Final estimation of fixed effects (with robust standard errors) ---------------------------------------------------------------------------- Standard Approx. Fixed Effect Coefficient Error T-ratio d.f. P-value ---------------------------------------------------------------------------- For INTRCPT1, B0 INTRCPT2, G00 11.741607 0.208945 56.195 157 0.000 SECTOR, G01 2.016592 0.331788 6.078 157 0.000 MEANSES, G02 * 2.654259 0.253568 10.468 157 0.000 For SES slope, B1 INTRCPT2, G10 3.159636 0.158565 19.926 158 0.000 SECTOR, G11 -2.096300 0.240992 -8.699 158 0.000 ---------------------------------------------------------------------------- The "*" gammas have been constrained. See the table on the header page. Final estimation of variance components: ----------------------------------------------------------------------------- Random Effect Standard Variance df Chi-square P-value Deviation Component ----------------------------------------------------------------------------- INTRCPT1, U0 1.84024 3.38650 157 787.30255 0.000 SES slope, U1 0.60746 0.36901 157 192.72983 0.027 level-1, R 6.06228 36.75129 ----------------------------------------------------------------------------- Statistics for current covariance components model -------------------------------------------------- Deviance = 46567.491225 Number of estimated parameters = 9
4. Level-1 variable as a random effect but not as a fixed effect
Sometimes, we may want to model a level-1 variable only as a random effect. For example, the effect of gender, on average, is not significant, as possibly shown below. In this case, we may not want to estimate the fixed effect of the variable female. Instead, we only use the variable female to model the variance.

Summary of the model specified (in equation format) ---------------------------------------------------
Level-1 Model
Y = B0 + B1*(FEMALE) + B2*(SES) + R
Level-2 Model B0 = G00 + G01*(SECTOR) + G02*(meanses) + U0 B1 = U1 B2 = G20 + G21*(SECTOR) + G22*(meanses) + U2 Level-1 OLS regressions -----------------------
Level-2 Unit intrcpt1 FEMALE slope SES slope ------------------------------------------------------------------------------ 1224 10.94364 -2.06161 2.64284 1288 13.01384 1.12946 3.35269 1296 8.51189 -1.35628 1.00858 1358 11.32162 -0.31470 4.98310 1374 10.94983 -2.63062 3.85439 1436 19.48721 -4.03507 2.58733 1461 17.50503 -1.15047 6.28572
Sigma_squared = 36.32580
Standard Error of Sigma_squared = 0.62429
Tau intrcpt1,B0 3.56382 -2.00755 0.33526 FEMALE,B1 -2.00755 2.32409 -0.23060 SES,B2 0.33526 -0.23060 0.10378
Standard Errors of Tau intrcpt1,B0 0.62400 0.57492 0.26957 FEMALE,B1 0.57492 0.72587 0.28483 SES,B2 0.26957 0.28483 0.21197
Tau (as correlations) intrcpt1,B0 1.000 -0.698 0.551 FEMALE,B1 -0.698 1.000 -0.470 SES,B2 0.551 -0.470 1.000
---------------------------------------------------- Random level-1 coefficient Reliability estimate ---------------------------------------------------- intrcpt1, B0 0.643 FEMALE, B1 0.384 SES, B2 0.052 ----------------------------------------------------
Note: The reliability estimates reported above are based on only 123 of 160 units that had sufficient data for computation. Fixed effects and variance components are based on all the data.
The value of the likelihood function at iteration 289 = -2.323661E+004
Final estimation of fixed effects: ---------------------------------------------------------------------------- Standard Approx. Fixed Effect Coefficient Error T-ratio d.f. P-value ---------------------------------------------------------------------------- For intrcpt1, B0 INTRCPT2, G00 11.933404 0.187148 63.764 157 0.000 SECTOR, G01 1.180992 0.293859 4.019 157 0.000 meanses, G02 5.281064 0.353685 14.932 157 0.000 For SES slope, B2 INTRCPT2, G20 2.875972 0.155149 18.537 157 0.000 SECTOR, G21 -1.615421 0.239356 -6.749 157 0.000 meanses, G22 1.033760 0.298472 3.464 157 0.001 ----------------------------------------------------------------------------
The outcome variable is mathach
Final estimation of fixed effects (with robust standard errors) ---------------------------------------------------------------------------- Standard Approx. Fixed Effect Coefficient Error T-ratio d.f. P-value ---------------------------------------------------------------------------- For intrcpt1, B0 INTRCPT2, G00 11.933404 0.173443 68.803 157 0.000 SECTOR, G01 1.180992 0.302841 3.900 157 0.000 meanses, G02 5.281064 0.330903 15.960 157 0.000 For SES slope, B2 INTRCPT2, G20 2.875972 0.146171 19.675 157 0.000 SECTOR, G21 -1.615421 0.236022 -6.844 157 0.000 meanses, G22 1.033760 0.328717 3.145 157 0.002 ----------------------------------------------------------------------------
Final estimation of variance components: ----------------------------------------------------------------------------- Random Effect Standard Variance df Chi-square P-value Deviation Component ----------------------------------------------------------------------------- intrcpt1, U0 1.88781 3.56382 120 326.18770 0.000 FEMALE slope, U1 1.52450 2.32409 123 187.64867 0.000 SES slope, U2 0.32214 0.10378 120 122.76674 0.413 level-1, R 6.02709 36.32580 -----------------------------------------------------------------------------
Note: The chi-square statistics reported above are based on only 123 of 160 units that had sufficient data for computation. Fixed effects and variance components are based on all the data.
Statistics for current covariance components model -------------------------------------------------- Deviance = 46473.216028 Number of estimated parameters = 13
5. Testing multi-degree-of-freedom variables
When using categorical predictor variables that have more than two levels, you will want to obtain an overall test of the variable. That is, you will want to know if the categorical variable, taken together, is statistically significant. As in OLS regression, if the whole categorical variable (i.e., the multi-degree-of-freedom test) is not statistically significant, you will not want to interpret any of the single degree-of-freedom tests of the dummy variables.

6. Using sampling weights
In the HLM manual, probability weights are called design weights. HLM can handle weights at both level 1 and level 2. If you have only a single final sampling weight, specify it as a level 1 variable. HLM cannot handle other elements that might be present in a survey data set, such as PSUs, stratification or replicate weights.
To specify sampling weights at level 1 or level 2, click on Other Settings, and then Estimation Settings, and then on the Weighting button.
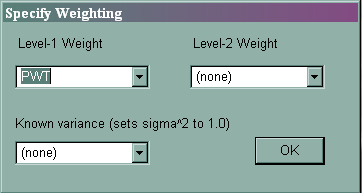
7. Using multiply imputed data
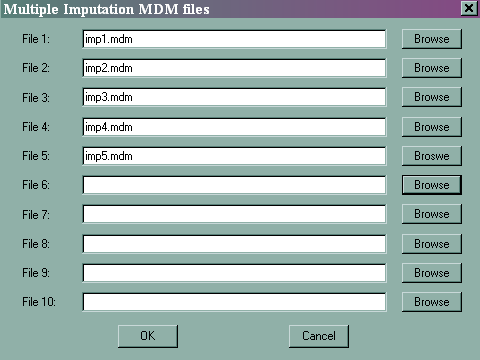
HLM cannot create multiply imputed data sets, but it can analyze them. HLM can handle only 10 imputed data sets. You must create an .mdm file for each of the multiply imputed data sets, and you must make exactly the same variable selections in each of the data sets.
To specify the multiply imputed data sets, click on Other Settings, and then Estimation Settings, and then on the Multiple imputation button.
Conclusions
HLM has some very nice features for the analysis of multilevel data.
- It has a very intuitive interface for building the model using a multi-equation format. The mixed button is a nice way to see the mixed equation (the combination of the multiple equations).
- It can create graphs to aid in the interpretation of cross-level interactions.
- While it does not have built in features for producing diagnostic plots, it easily generates the diagnostic data for use in common statistical packages.
- HLM is very flexible in its ability to read in data. In older versions of HLM, you needed to create a level 1 and a level 2 data file, but with the current version, you can both level 1 and level 2 variables in a single data file. You can easily read in SPSS and Stata data files, as well data in several other formats.
- We have not discussed many of the other types of analysis that HLM can do, such as three-level models, non-linear models, and cross-classified models.
References
Multilevel Analysis: An Introduction to Basic and Advanced Multilevel Modeling by Tom Snijders and Roel Bosker
Introduction to Multilevel Modeling by Ita Kreft and Jan de Leeuw
Multilevel Analysis: Techniques and Applications by Joop Hox
Hierarchical Linear Models, Second Edition by Stephen Raudenbush and Anthony Bryk
HLM 6 – Hierarchical Linear and Nonlinear Modeling by Raudenbush, et al.
Multilevel Analysis for Applied Research: It's Just Regression! by Robert Bickel
Power and Sample Size in Multilevel Modeling by Tom Snijders (in Encyclopedia of Statistics in Behavioral Science, Everitt and Howell (editors), Vol. 3, 1570-1573)
littletonthembleavelf.blogspot.com
Source: https://stats.oarc.ucla.edu/other/hlm/hlm-mlm/introduction-to-multilevel-modeling-using-hlm/
0 Response to "Hlm Missing Data Found at Level 1 Unable to Continue"
Post a Comment